I was curious how the game would play out over multiple rounds, since it varied greatly from match to match, so I created a simulation that would recreate a full game with six players. Then I had it play 50,000 games, and it kept track of how many rolls it took to complete the game, and which player won the game. Player 1 always started the game, and play went in order (Player 1, Player 2, Player 3, etc.)
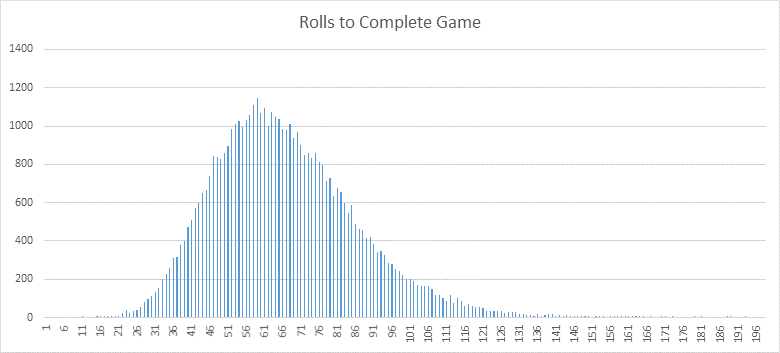
Here's the distribution of rolls required to complete each game:
So if you're hoping for a quick game there's a slim chance you'll finish in 25 rolls or less, you're more likely to take 60 rolls, and it's possible you're in for the long haul of 190 rolls!
Here's the distribution of winning players from each game:
I was expecting a more even distribution here, so this came as a surprise. It turns out if you really want to win then you should make sure not to be among the first players in the round. Apparently there may be some strategy involved in this game of chance after all.

No comments:
Post a Comment